Analysis for the Lifestyle Channel

Maks Nikiforov and Mark Austin Due 10/31/2021

Data Import
Introduction
Summarizations
Modeling
Model Comparisons
References

##For markdown automation need a different 
##  image and cache folder 
##  for each of the 6 channels so that results
##    from different channels don't overwrite each other
##Also setting up currentChannel variable 
if (params$channel=="data_channel_is_bus") {
  knitr::opts_chunk$set(fig.path = "images/bus/",
                        cache.path = "cache/bus/")
  currentChannel<-"Business"
} else if (params$channel=="data_channel_is_entertainment") {
  knitr::opts_chunk$set(fig.path = "images/entertainment/",
                        cache.path="cache/entertainment/")
  currentChannel<-"Entertainment"
} else if (params$channel=="data_channel_is_lifestyle") {
  knitr::opts_chunk$set(fig.path = "images/lifestyle/",
                        cache.path = "cache/lifestyle/")
  currentChannel<-"Lifestyle"
} else if (params$channel=="data_channel_is_socmed") {
  knitr::opts_chunk$set(fig.path = "images/socmed/",
                        cache.path = "cache/socmed/")
  currentChannel<-"Social Media"
} else if (params$channel=="data_channel_is_tech") {
  knitr::opts_chunk$set(fig.path = "images/tech/",
                        cache.path = "cache/tech/")
  currentChannel<-"Tech"
} else if (params$channel=="data_channel_is_world") {
  knitr::opts_chunk$set(fig.path = "images/world/",
                        cache.path = "cache/world/")
  currentChannel<-"World"
} 

Data Import

Data was imported first to allow for a more automated introduction.

# Read all data into a tibble
fullData<-read_csv("./data/OnlineNewsPopularity.csv")

# Eliminate non-predictive variables
reduceVarsData<-fullData %>% select(-url,-timedelta)

#test code for pre markdown automation
#params$channel<-"data_channel_is_bus"

#filter by the current params channel
channelData<-reduceVarsData %>% filter(eval(as.name(params$channel))==1) 

# URL data for top ten articles in each category
channelDataURL <- fullData %>% filter(eval(as.name(params$channel))==1)

###Can now drop the data channel variables 
channelData<-channelData %>% select(-starts_with("data_channel"))

Introduction

This page offers an exploratory data analysis of Lifestyle articles in the online news popularity data set. The top ten articles in this category, based on the number of shares on social media, include the following titles:

Shares	Article title
208300	Obama to Discuss NSA Reform With Lawmakers
196700	No Movie Trailer Is Complete Without This One Line
139600	87% of American Teenagers Send Text Messages Each Month
81200	High-Tech Wristband Monitors Mood
73100	22 Books for Your Ultimate Summer Reading List
56000	Finalists Exhibit Tech for $465 Million Virtual Border Fence
54900	Cybersecurity Experts Will Face Off in Mock NetWars
54200	84% of Smartphone Owners Use Apps While Getting Ready in the Morning
49700	It’s Still Easy to Get Away With Revenge Porn
45100	Beats Solo² Headphones Sound Great, But You’re Paying for Fashion

Two variables - url and timedelta - are non-predictive and have been removed. The remaining 53 variables comprise 2099 observations, which makes up 5.3 percent of the original data set. Fernandes et al., who sourced the data, concentrated on article characteristics such as verbosity and the polarity of content, publication day, the quantity of included media, and keyword attributes (Fernandes et al., 2015). A subset of these variables and the correlations between them are explored in subsequent sections.

The broader purpose of this analysis is predicated on using supervised learning to predict a target variable - shares. To this end, the final sections outline four unique models for conducting such predictions and an assessment of their relative performance. Two models are rooted in multiple linear regression analysis, which assesses relationships between a response variable and two or more predictors. The remaining models are based on random forest and boosted tree techniques. The random forest method averages results from multiple decision trees which are fitted with a random parameter subset. The boosted tree method spurns averages in favor of results that stem from weighted iterations (James et al., 2021).

Summarizations

Numerical Summaries

The first table summarizes information for article shares grouped by whether an article was a weekend article or not. This summary gives an idea of the center and spread of shares across type of day group levels.

channelData %>% 
  mutate(dayType=ifelse(is_weekend,"Weekend","Weekday")) %>%
  group_by(dayType) %>% 
  summarise(Avg = mean(shares), Sd = sd(shares), 
    Median = median(shares), IQR =IQR(shares)) %>% kable()

dayType	Avg	Sd	Median	IQR
Weekday	3628.255	9551.749	1600	2050
Weekend	3916.696	5044.188	2100	2600

The next tables gives expands on the idea of the first table by grouping shares by each day of the week. This summary gives an idea of the center and spread of shares across day of the week group levels.

dowData<-channelData %>% select(starts_with("weekday_is"),shares) %>%
  mutate(dayofWeek=case_when(as.logical(weekday_is_monday)~"Monday",
                             as.logical(weekday_is_tuesday)~"Tuesday",
                             as.logical(weekday_is_wednesday)~"Wednesday",
                             as.logical(weekday_is_thursday)~"Thursday",
                             as.logical(weekday_is_friday)~"Friday",
                             as.logical(weekday_is_saturday)~"Saturday",
                             as.logical(weekday_is_sunday)~"Sunday")) %>%
  select(dayofWeek,shares)

dowLevels<-c("Monday","Tuesday","Wednesday",
             "Thursday","Friday","Saturday","Sunday")
dowData$dayofWeek<-factor(dowData$dayofWeek,levels = dowLevels)

dowData %>%  
  group_by(dayofWeek) %>% 
  summarise(Avg = mean(shares), Sd = sd(shares), 
    Median = median(shares), IQR =IQR(shares)) %>% kable()

dayofWeek	Avg	Sd	Median	IQR
Monday	4345.711	14072.938	1600	2575.00
Tuesday	4152.494	13544.476	1500	1975.00
Wednesday	3173.180	5608.013	1600	1800.25
Thursday	3500.268	5820.627	1600	2250.00
Friday	3025.869	4539.610	1500	2000.00
Saturday	4062.451	5350.749	2100	2650.00
Sunday	3790.376	4771.926	2100	2675.00

The table below highlights variables with the highest and most significant correlations in the data set. This output may be considered when analyzing covariance to control for potentially confounding variables.

# Display top 10 highest correlations
covarianceDF <- corr_cross(df = channelData, max_pvalue = 0.05, top = 10, plot = 0) %>% 
  select(key, mix, corr, pvalue) %>% rename("Variable 1" = key, "Variable 2" = mix, 
                                            "Correlation" = corr, "p-value" = pvalue) 

# Display non-zero p-values
covarianceDF[4] <- format.pval(covarianceDF[4])

kable(covarianceDF)

Variable 1	Variable 2	Correlation	p-value
kw_max_min	kw_avg_min	0.956574	< 2.22e-16
self_reference_max_shares	self_reference_avg_sharess	0.911916	< 2.22e-16
n_unique_tokens	n_non_stop_unique_tokens	0.906660	< 2.22e-16
n_non_stop_words	average_token_length	0.870183	< 2.22e-16
kw_min_min	kw_max_max	-0.856370	< 2.22e-16
kw_max_avg	kw_avg_avg	0.818423	< 2.22e-16
global_rate_negative_words	rate_negative_words	0.815529	< 2.22e-16
self_reference_min_shares	self_reference_avg_sharess	0.787590	< 2.22e-16
kw_max_max	kw_avg_max	0.750110	< 2.22e-16
rate_positive_words	rate_negative_words	-0.731286	< 2.22e-16

Contingency Table

The following contingency table displays counts and sums for the number of article shares within given ranges by the day of week shared. Share ranges were selected to illustrate lower, medium, and higher ranges of shares. Examining these counts can show possible patterns of shares by day or week and the range grouping for shares.

##dig.lab is needed to avoid R defaulting to scientific notation
kable(addmargins(table
                 (dowData$dayofWeek,cut(dowData$shares,
                  c(0,200,1000,10000,860000),dig.lab = 7))))

	(0,200]	(200,1000]	(1000,10000]	(10000,860000]	Sum
Monday	3	81	213	25	322
Tuesday	1	86	229	18	334
Wednesday	3	106	254	25	388
Thursday	3	87	241	27	358
Friday	3	76	210	16	305
Saturday	0	9	156	17	182
Sunday	0	17	180	13	210
Sum	13	462	1483	141	2099

Plots

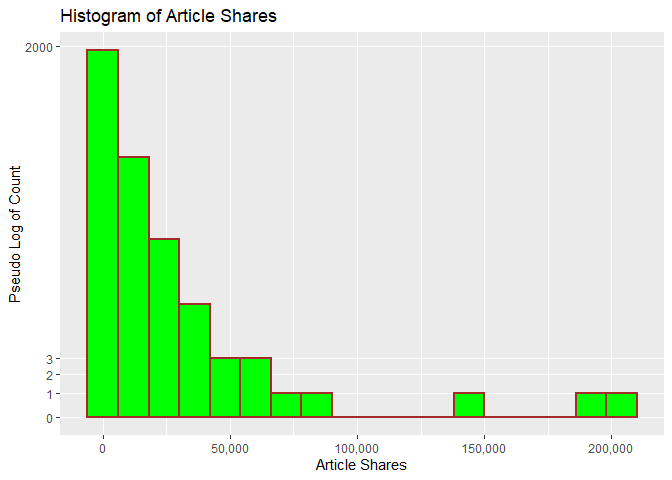
The following histogram looks at the distribution of shares. A pseudo log y scale with modified y break values was used so that article shares with low frequency will appear. We can tell from the histogram whether shares has a symmetric or skewed distribution. The distribution is symmetric if the tails are the same around the center. The distribution is right skewed if there is a long left tail and right skewed if there is a long right tail.

###creating histogram of shares data 
##scales comma was used to avoid the default scientific notation
##pseudo log with breaks was used to make low frequency values 
## more visisble
g <- ggplot(channelData, aes( x = shares))
g + geom_histogram(binwidth=12000,color = "brown", fill = "green", 
  size = 1)  + labs(x="Article Shares", y="Pseudo Log of Count",
  title = "Histogram of Article Shares") +
  scale_y_continuous(trans = "pseudo_log",
                     breaks = c(0:3, 2000, 6000),minor_breaks = NULL) +
  scale_x_continuous(labels = scales::comma) 

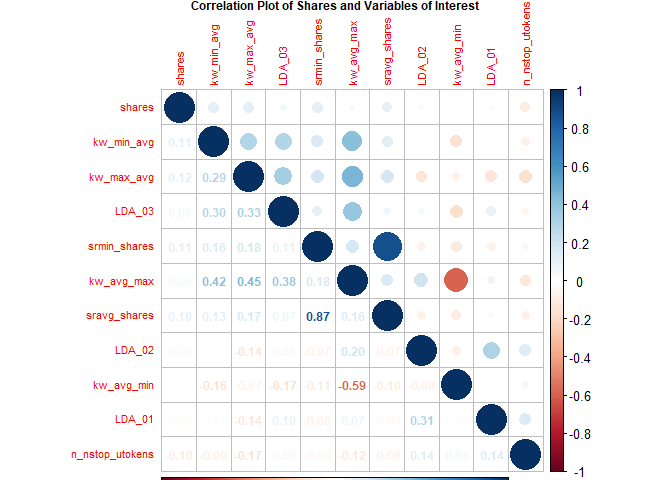
Fernandes et al. highlight several variables in their random forest model (Fernandes et al., 2015). The following variables from their top 11 were included in the following correlation plot with variables in () being renamed for this plot: shares,kw_min_avg,kw_max_avg,LDA_03,self_reference_min_shares(srmin_shares),kw_avg_max,self_reference_avg_sharess(sravg_shares),LDA_02,kw_avg_min,LDA_01,n_non_stop_unique_tokens(n_nstop_utokens).
The plot shows correlation with the response variable shares and the other various combinations. Larger circles indicate stronger positive (blue) or negative (red) correlation with correlation values on the lower portion of the plot.

##Reduce variable name length for later plotting
## Otherwise var names overwrite Title no matter
##  how many other size tweaks were made
corrData<-channelData %>% 
  mutate(sravg_shares=self_reference_avg_sharess,
         srmin_shares=self_reference_min_shares,
         n_nstop_utokens=n_non_stop_unique_tokens)

Correlation<-cor(select(corrData, shares, kw_min_avg,
        kw_max_avg, LDA_03, srmin_shares,
        kw_avg_max, sravg_shares, LDA_02,
        kw_avg_min, LDA_01, n_nstop_utokens),
        method = "spearman")

corrplot(Correlation,type="upper",tl.pos="lt", tl.cex = .70)
corrplot(Correlation,type="lower",method="number",
         add=TRUE,diag=FALSE,tl.pos="n",tl.cex = .70,number.cex = .75,
         title = 
           "Correlation Plot of Shares and Variables of Interest",
         mar=c(0,0,.50,0),cex.main = .75)

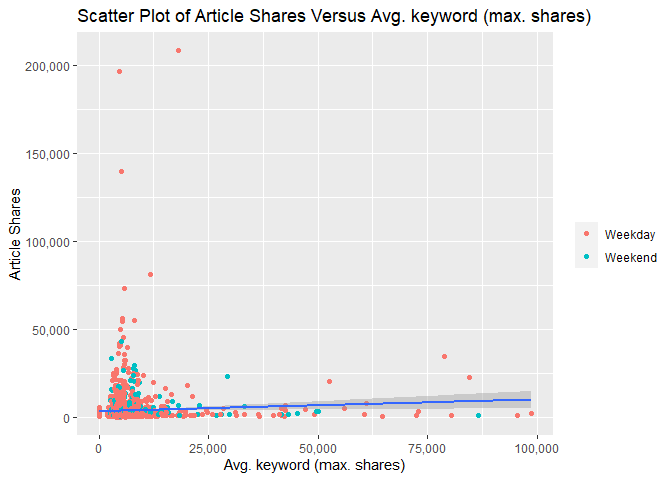
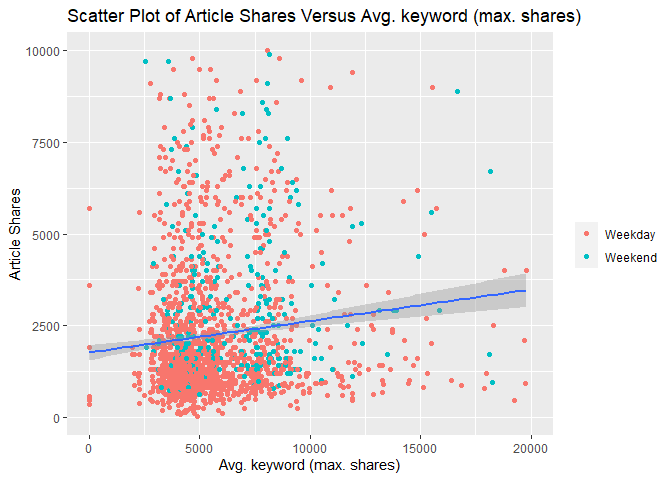
The following two scatterplots illustrate the relationship between response article shares shares and predictor average keyword (max shares) kw_max_ave. kw_max_ave was chosen because it was one of the potential predictors examined in the previous correlation plot.

Both scatterplots plot these variables and add a simple linear regression line to the graph.

For either graph, an upward relationship indicates higher average keyword values tend towards more article shares. A negative relation would indicate a lower average keyword values tend towards more article shares.

In addition, both graphs use differing color for weekday and weekend articles so that we can spot any possible trends with those values too.

The first scatterplot uses the default R generated axes so that potential outliers or significant observations can be observed.

The second scatterplot reduces the scale of both axes to make it easier to spot relationships for the majority of data that occur within these bounds.

###Create new factor version of weekend variable 
### to use later in graphs
scatterData<-channelData %>% 
  mutate(dayType=ifelse(is_weekend,"Weekend","Weekday"))
scatterData$dayType<-as.factor(scatterData$dayType)

###First scatter plot with ALL data 
g<-ggplot(data = scatterData,
          aes(x= kw_max_avg,y=shares))
g + geom_point(aes(color=dayType)) +
  geom_smooth(method = lm) +
  scale_y_continuous(labels = scales::comma) +
  scale_x_continuous(labels = scales::comma) +
  labs(x="Avg. keyword (max. shares)", y="Article Shares",
       title = "Scatter Plot of Article Shares Versus Avg. keyword (max. shares)",color="") 

###Second scatter plot with reduced axes
g<-ggplot(data = scatterData,
          aes(x= kw_max_avg,y=shares))
g + geom_point(aes(color=dayType)) +
  geom_smooth(method = lm) +
  ylim(0,10000) +
  xlim(0,20000) +
    labs(x="Avg. keyword (max. shares)", y="Article Shares",
       title = "Scatter Plot of Article Shares Versus Avg. keyword (max. shares)",
       color="")

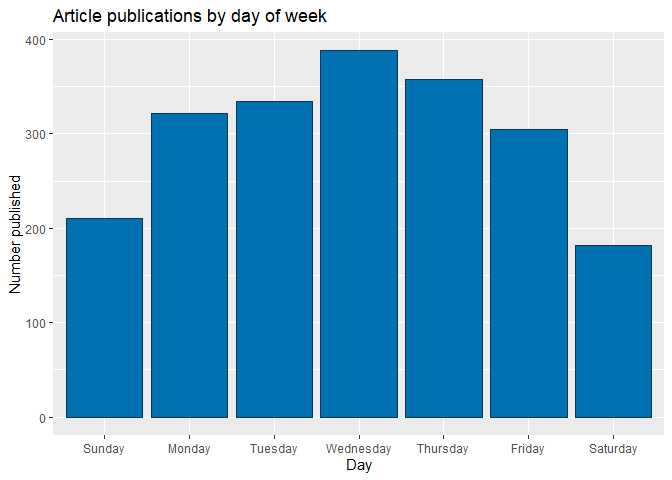
The bar plot below shows cumulative article publications for each day of the week, with higher bars indicating more publications. However, days with the largest number of publications are not necessarily ones with the most article shares, as seen in the subsequent box plot.

# Subset columns to include only weekday_is_*
weekdayData <- channelData %>% select(starts_with("weekday_is"))

# Calculate sum of articles published in each week day
articlesPublished <- lapply(weekdayData, function(c) sum(c=="1"))

# Use factor to set specific order in bar plot
weekPubDF <- data.frame(weekday=c("Monday", "Tuesday", "Wednesday", 
                           "Thursday", "Friday", "Saturday", "Sunday"),
                count=articlesPublished)
weekPubDF$weekday = factor(weekPubDF$weekday, levels = c("Sunday", "Monday", "Tuesday", "Wednesday", 
                           "Thursday", "Friday", "Saturday"))

# Create bar plot with total publications by day
weekdayBar <- ggplot(weekPubDF, aes(x = weekday, y = articlesPublished)) + geom_bar(stat = "identity", color = "#123456", fill = "#0072B2") 
weekdayBar + labs(x = "Day", y = "Number published",
       title = "Article publications by day of week")

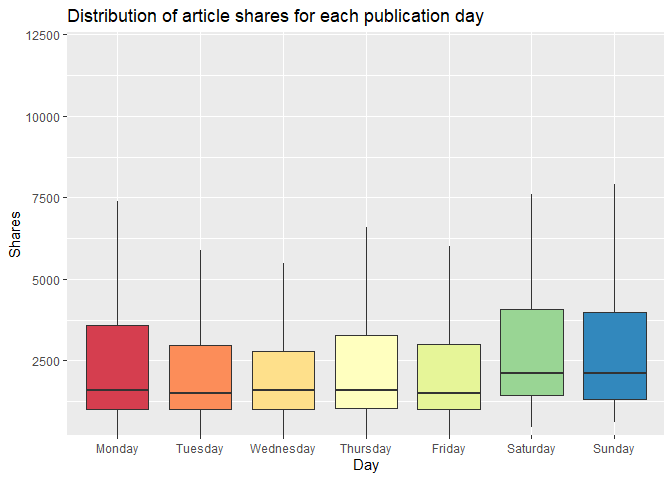
The boxplot below examines the day of article publication (Monday-Sunday) and the associated distribution of article shares. The median line indicates the center of the distribution of shares, and comparatively high medians indicate days that have relatively high circulation of Mashable articles in social media networks. For days in which the median is closer to the lower quartile (and where the upper whisker may be taller than the lower whisker), the distribution is skewed to the right. Conversely, a median that is closer to the upper quartile indicates a distribution that is skewed to the left. Days with relatively taller boxplots also have greater variability of shares.

# Subset columns to include only weekday_is_*, shares,
# create categorical variable, "day", denoting day of week (Mon-Sun)
medianShares <- channelData %>% select(starts_with("weekday_is"), shares) %>% mutate(day = NA)

# Populate "day"
for (i in 1:nrow(medianShares)) {
  if (medianShares$weekday_is_monday[i] == 1) {
    medianShares$day[i] = "Monday"
  }
  else if (medianShares$weekday_is_tuesday[i] == 1) {
    medianShares$day[i] = "Tuesday"
  }
  else if (medianShares$weekday_is_wednesday[i] == 1) {
    medianShares$day[i] = "Wednesday"
  }
  else if (medianShares$weekday_is_thursday[i] == 1) {
    medianShares$day[i] = "Thursday"
  }
  else if (medianShares$weekday_is_friday[i] == 1) {
    medianShares$day[i] = "Friday"
  }
  else if (medianShares$weekday_is_saturday[i] == 1) {
    medianShares$day[i] = "Saturday"
  }
  else if (medianShares$weekday_is_sunday[i] == 1) {
    medianShares$day[i] = "Sunday"
  }
  else {
    medianShares$day[i] = NA
  }
}

# Transform "day" into factor with levels to control order of boxplots
medianShares$day <- factor(medianShares$day, 
                           levels = c("Monday", "Tuesday", "Wednesday", 
                                      "Thursday", "Friday", "Saturday", "Sunday"))

# Plot distribution of shares for each day of the week
sharesBox <- ggplot(medianShares, aes(x = day, y = shares, fill = day))

sharesBox + geom_boxplot(outlier.shape = NA) + 
  # Exclude extreme outliers, limit range of y-axis
  coord_cartesian(ylim = quantile(medianShares$shares, c(0.1, 0.95))) +
  # Remove legend after coloration
  theme(legend.position = "none") +
  labs(x = "Day", y = "Shares",
       title = "Distribution of article shares for each publication day") + scale_fill_brewer(palette = "Spectral")

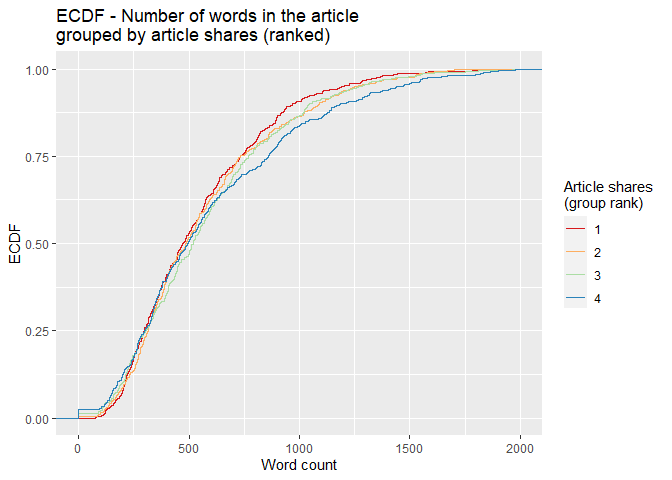
For the empirical cumulative distribution function (ECDF) below, the dplyr ranking function ntile() divides shares into four groups. Observations with the fewest shares are placed into group 1, those with the most shares are placed into group 4, and intermediaries reside in groups 2 and 3. The horizontal axis lists word count, and the vertical axis lists the percentage of content with that word count. A divergence of the colored lines suggests that the number of words differs in content with the fewest and most shares. At any given percentage of content (y-value), curves further to the right correspond to more words within the associated shares group. Groups with curves that are further to the left indicate fewer words in that percentage of content.

# Create variable to for binning the shares
binnedShares <- channelData %>% mutate(shareQuantile = ntile(channelData$shares, 4))
binnedShares <- binnedShares %>% mutate(totalMedia = num_imgs + num_videos)

# Render and label word count ECDF, group by binned shares
avgWordHisto <- ggplot(binnedShares, aes(x = n_tokens_content, colour = shareQuantile))
avgWordHisto + stat_ecdf(geom = "step", aes(color = as.character(shareQuantile))) +
  labs(title="ECDF - Number of words in the article \ngrouped by article shares (ranked)",
     y = "ECDF", x="Word count") + xlim(0,2000) + 
  scale_colour_brewer(palette = "Spectral", name = "Article shares \n(group rank)")

Modeling

Splitting Data

Per project requirements, the data for each channel are split with 70% of the data becoming training data and 30% of the data becoming test data.

#Using set.seed per suggestion so that work will be reproducible
set.seed(20)

dataIndex <-createDataPartition(channelData$shares, p = 0.7, list = FALSE)

channelTrain <-channelData[dataIndex,]
channelTest <-channelData[-dataIndex,]

Linear Regression Models

Linear regression models describe a linear relationship between a response variable and one or more explanatory variables. Models with one explanatory variable are called simple linear regression models and models with more than one explanatory variable are called multiple linear regression models. Multiple linear regression models can include polynomial and interaction terms. Each explanatory variable has an associated estimated parameter. All linear regression models are linear in the parameters.

For linear regression, explanatory variables can be continuous or categorical. However, response variables are only continuous for linear regression models.

Linear regression models are fit with training data by minimizing the sum of squared errors. Model fitting results in a line for simple linear regression and a saddle for multiple linear regression.

The first linear regression model contains predictors that encompass content keywords, sentiment and subjectivity, the length of content (the effects of which were gleaned previously from the ECDF), and link citations.

# Parallel cluster setup
cl <- makePSOCKcluster(6)
registerDoParallel(cl)

# Linear regression with subset of predictors (p-value < 0.1) selected after performing 
# least squares fit on the entire set of predictors. 
lmFit1 <- train(shares ~ kw_avg_avg + kw_max_avg + kw_min_avg + 
    num_hrefs + self_reference_min_shares + global_subjectivity + 
    num_self_hrefs + n_tokens_title + n_tokens_content + n_unique_tokens + 
    average_token_length + kw_min_max + num_keywords + kw_max_min + abs_title_subjectivity + 
    global_rate_positive_words, 
    data = channelTrain,
               method = "lm",
               preProcess = c("center", "scale"),
               trControl = trainControl(method = "cv", 
                                        number = 5))
stopCluster(cl)

The second linear regression model contains main effects for most of the predictors listed earlier in the correlation plot. If variables had more than .50 pairwise correlation in any channel, one variable of that pair was excluded. Excluded variables were: self_reference_min_shares, kw_avg_max, and LDA_01.

cl <- makePSOCKcluster(6)
registerDoParallel(cl)

lmFit2 <- train(shares ~ kw_min_avg +
        kw_max_avg + LDA_03 +  
        self_reference_avg_sharess + LDA_02 +
        kw_avg_min + n_non_stop_unique_tokens, 
               data = channelTrain,
               method = "lm",
               preProcess = c("center", "scale"),
               trControl = trainControl(method = "cv", 
                                        number = 10))


stopCluster(cl)

Random Forest Model

Random forest models aggregate results from many sample decision trees. Those sample trees are produced using bootstrap samples created using resampling with replacement. A tree is trained on each bootstrap sample, resulting in a prediction based on that training sample data. Results from all bootstrap samples are averaged to arrive at a final prediction.

Both bagging and random forest methods use bootstrap sampling with decision trees. However, bagging includes all predictors which can lead to less reduction in variance when strong predictors exist. Unlike bagging, random forests do not use all predictors but use a random subset of predictors for each bootstrap tree fit. Random forests usually have a better fit than bagging models.

In this particular case, the response shares is continuous and we are working with regression trees. The mtry tuning parameter controls how many random predictors are used in the bootstrap samples. An mtry of 1 to 30 was chosen as a way to evaluate up to 30 predictors. These values were chosen to work within available computing constraints. Five fold cross validation is used to choose the optimal mtry value corresponding to the lowest RMSE.

##Run time presented a challenge so parallel processing was used
##Followed Parallel instructions on caret page
##   https://topepo.github.io/caret/parallel-processing.html

##Various mtry values were tried with a 20 minute runtime goal
##  A 20 minute per channel runtime corresponds 
##  to a total of about 2 hours model fit for all 6 channels

##mtry 1:30 was chosen because it was close to 20 minutes
##mtry 1:20 had 10 minute runtime and 1:30 took 30 minutes

##repeatedcv was evaluated but took over 30 minutes 
## thus repeats were not used


cl <- makePSOCKcluster(6)
registerDoParallel(cl)

rfFit <- train(shares ~ ., data = channelTrain,
               method = "rf",
               preProcess = c("center", "scale"),
               trControl = trainControl(method = "cv",
                                number = 5),
               tuneGrid = data.frame(mtry = 1:30))

stopCluster(cl)

rfFit

## Random Forest 
## 
## 1472 samples
##   52 predictor
## 
## Pre-processing: centered (52), scaled (52) 
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 1178, 1176, 1178, 1177, 1179 
## Resampling results across tuning parameters:
## 
##   mtry  RMSE      Rsquared     MAE     
##    1    7700.354  0.011448227  3257.875
##    2    7767.243  0.010557108  3344.202
##    3    7818.160  0.008819996  3361.536
##    4    7863.695  0.008708639  3392.410
##    5    7885.215  0.009835263  3415.104
##    6    7903.022  0.010214064  3396.174
##    7    7989.386  0.009209833  3452.842
##    8    8044.493  0.007095766  3463.653
##    9    8072.146  0.006458376  3464.451
##   10    8133.106  0.006624797  3476.167
##   11    8154.974  0.007672426  3486.552
##   12    8140.628  0.010311884  3481.164
##   13    8151.268  0.009191298  3482.209
##   14    8219.685  0.007071879  3495.295
##   15    8266.071  0.007106738  3499.214
##   16    8272.007  0.007487571  3485.774
##   17    8335.853  0.006336330  3522.780
##   18    8343.314  0.007765418  3525.826
##   19    8403.869  0.007720668  3517.991
##   20    8406.939  0.006405060  3545.463
##   21    8422.275  0.008047622  3516.312
##   22    8451.770  0.006368502  3537.152
##   23    8488.364  0.007367648  3524.590
##   24    8454.638  0.006303017  3522.232
##   25    8526.539  0.007246372  3520.831
##   26    8582.794  0.006213899  3544.972
##   27    8627.369  0.006609938  3544.678
##   28    8647.981  0.006894932  3552.627
##   29    8631.074  0.007435105  3541.756
##   30    8678.797  0.006936974  3545.583
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was mtry = 1.

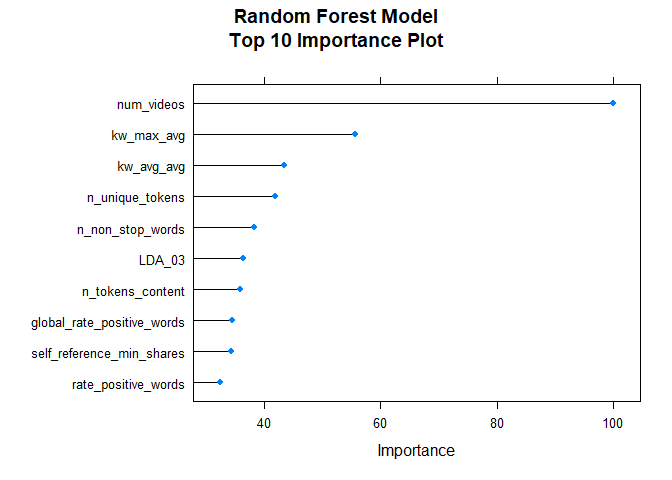
After fitting the random forest model, the following variable importance plot is created. The top ten most important predictors are plotted using a scale of 0 to 100.

rfImp <- varImp(rfFit, scale = TRUE)
plot(rfImp,top = 10, main="Random Forest Model\nTop 10 Importance Plot")

Boosted Tree Model

Boosting is a general method whereby decision trees are grown sequentially using residuals (the differences between observed values and predicted values of a variable) as the response. Initial prediction values start at 0 for all combinations of predictors, so that the first set of residuals matches the observed values in our data. To mitigate low bias and high variance, contributions from subsequent trees are scaled with a shrinkage parameter, λ. The value of this parameter is generally small (0.01 or 0.001), which slows tree growth and tampers overfitting (James et al., 2021).

# Re-allocate cores for parallel computing
cl <- makePSOCKcluster(6)
registerDoParallel(cl)


# Boosted tree fit with tuneLength (let function decide parameter combinations)
boostedTreeFit <- train(shares ~ ., data = channelTrain,
               method = "gbm",
               preProcess = c("center", "scale"),
               trControl = trainControl(method = "cv", 
                                        number = 5),  
               tuneLength = 5)

## Iter   TrainDeviance   ValidDeviance   StepSize   Improve
##      1 81592531.7691             nan     0.1000 -110219.7078
##      2 81125745.4982             nan     0.1000 -171529.4904
##      3 81064940.7366             nan     0.1000 -41573.2315
##      4 80930623.3187             nan     0.1000 138028.7523
##      5 80553322.6423             nan     0.1000 -87917.9221
##      6 80288738.6406             nan     0.1000 -126909.0245
##      7 80070259.2664             nan     0.1000 -264937.3073
##      8 79967993.4034             nan     0.1000 -82901.7624
##      9 79932628.1262             nan     0.1000 -47379.8320
##     10 79723983.2571             nan     0.1000 -52377.8386
##     20 78302534.7038             nan     0.1000 -285124.4793
##     40 77803375.1027             nan     0.1000 -223603.4316
##     50 77553134.0175             nan     0.1000 -415020.9452

# Define tuning parameters based on $bestTune from the permutations above
nTrees <- boostedTreeFit$bestTune$n.trees
interactionDepth = boostedTreeFit$bestTune$interaction.depth
minObs = boostedTreeFit$bestTune$n.minobsinnode
shrinkParam <- boostedTreeFit$bestTune$shrinkage

# Boosted tree fit with defined parameters
bestBoostedTree <- train(shares ~ ., data = channelTrain,
               method = "gbm",
               preProcess = c("center", "scale"),
               trControl = trainControl(method = "cv", 
                                        number = 5),  
               tuneGrid = expand.grid(n.trees = nTrees, interaction.depth = interactionDepth,
                                      shrinkage = shrinkParam, n.minobsinnode = minObs))

## Iter   TrainDeviance   ValidDeviance   StepSize   Improve
##      1 81970919.4694             nan     0.1000 33269.3045
##      2 81544792.4778             nan     0.1000 -44965.6893
##      3 80990983.9297             nan     0.1000 12946.2311
##      4 80710153.3339             nan     0.1000 -61735.7828
##      5 80505886.1632             nan     0.1000 -84920.5351
##      6 80223864.9008             nan     0.1000 -102302.6449
##      7 79996735.8107             nan     0.1000 -176239.8212
##      8 79791678.7133             nan     0.1000 -92517.9657
##      9 79674421.6124             nan     0.1000 -114856.9453
##     10 79455266.6071             nan     0.1000 -144634.3177
##     20 78447467.1908             nan     0.1000 -46217.4624
##     40 77584239.2316             nan     0.1000 -154797.5720
##     50 76942816.5418             nan     0.1000 210463.3425

stopCluster(cl)

Model Comparisons

After models were fit with training data, we do predictions with testing data. Finally, RMSE metrics are extracted and compared. The model with lowest RMSE is presented as the winning model.

# Predict using test data
predictLM1 <- predict(lmFit1, newdata = channelTest)

# Metrics
RMSELM1 <- postResample(predictLM1, obs = channelTest$shares)["RMSE"][[1]]
RMSELM1

## [1] 8344.936

# Store value for model comparison
modelPerformance <- tibble(RMSE = RMSELM1, Model = "Linear regression 1")

predictLM2 <- predict(lmFit2, newdata = channelTest)
RMSELM2<-postResample(predictLM2, channelTest$shares)["RMSE"][[1]]
RMSELM2

## [1] 8450.339

modelPerformance <- add_row(modelPerformance, RMSE = RMSELM2, Model = "Linear regression 2")

predictRF <- predict(rfFit, newdata = channelTest)
RMSERF<-postResample(predictRF, channelTest$shares)["RMSE"]
RMSERF

##     RMSE 
## 8415.603

modelPerformance <- add_row(modelPerformance, RMSE = RMSERF, Model = "Random forest")

# Predict using test data
predictGBM <- predict(bestBoostedTree, newdata = channelTest)

# Metrics
RMSEGBM <- postResample(predictGBM, obs = channelTest$shares)["RMSE"]
RMSEGBM

##     RMSE 
## 8503.737

modelPerformance <- add_row(modelPerformance, RMSE = RMSEGBM, Model = "Boosted tree")

# Select row with lowest value of RMSE.
selectModel <- modelPerformance %>% slice_min(RMSE)
selectModel

## # A tibble: 1 x 2
##    RMSE Model              
##   <dbl> <chr>              
## 1 8345. Linear regression 1

Based on the preceding analyses with test data, the Linear regression 1 model yields the lowest RMSE - 8344.9359123.

References

Fernandes, K., Vinagre, P., & Cortez, P. (2015). A proactive intelligent decision support system for predicting the popularity of online news. In F. Pereira, P. Machado, E. Costa, & A. Cardoso (Eds.), *Progress in artificial intelligence* (pp. 535–546). Springer International Publishing.

James, G., Witten, D., Hastie, T., & Tibshirani, R. (2021). *An introduction to statistical learning*. Springer US. <https://doi.org/10.1007/978-1-0716-1418-1>